部分預應力梁開裂以后截面平均應變和剛度的直接計算法
項劍鋒 碩士、教授級高級工程師
(浙江省建筑科學設計研究院、浙江劍鋒加固工程有限公司)
提 要:本文基于截面平均應變符合平截面假定,截面彎矩與受拉邊緣處平均應變及截面曲率與受拉邊緣處平均應變的雙折線關系,利用部分預應力梁開裂以后不考慮受拉砼作用時截面上的彎矩—曲率—應變的簡化線性關系式,直接導出了開裂以后考慮受拉砼作用時截面平均應變和剛度的精度很高又很簡捷的計算公式,并通過計算例題使計算方法更加明了。
關鍵詞:彎矩、曲率、截面平均應變、雙折線、剛度、直接計算、計算例題 1 前言
在作預應力梁和鋼筋混凝土梁的撓度和裂縫寬度驗算時,主要的計算內容是開裂以后的截面平均應變和剛度。由于截面開裂以后,裂縫之間和裂縫頂部的受拉區混凝土還要承擔一部分拉力,而這部分拉力的大小和在加荷過程中的衰減速度均受許多因素影響,所以使得開裂以后的截面平均應變和剛度計算變得較為困難。
我國現行混凝土結構設計規范(GB50010-2002)采用將裂縫截面上縱向受拉鋼筋的應力(鋼筋混凝土梁)或等效應力(預應力混凝土梁)除鋼筋彈性模量乘應變不均勻系數的方法計算鋼筋重心處的截面平均應變值。裂縫截面上縱向受拉鋼筋的應力或等效應力采用簡化的內力臂計算公式計算。梁的剛度是基于彎矩曲率的雙折線假定,利用試驗資料求出  時的剛度降低系數β0.4的擬合近似值,再利用幾何關系導出M = Mk時綜合剛度的近似計算公式。 時的剛度降低系數β0.4的擬合近似值,再利用幾何關系導出M = Mk時綜合剛度的近似計算公式。
規范的這種方法,具有下述幾點不足之處:
1、簡化的內力臂計算公式沒有正確地反映內力臂與有關參數的函數關系。根據開裂截面彈性理論計算公式導出的高精度簡化式[1]知,內力臂與KS及rs二個參數成線性關系,與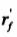 不成線性關系(Ks為縱向受拉鋼筋換算截面重心至受拉邊緣的距離與h的比值,rs為受拉鋼筋換算面積與bh的比值, 不成線性關系(Ks為縱向受拉鋼筋換算截面重心至受拉邊緣的距離與h的比值,rs為受拉鋼筋換算面積與bh的比值,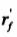 為受壓翼緣截面面積與bh的比值)。而規范公式的內力臂與 為受壓翼緣截面面積與bh的比值)。而規范公式的內力臂與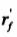 成線性關系,與ks和rs二個參數無關。 成線性關系,與ks和rs二個參數無關。
2、規范的方法只能計算縱向受拉鋼筋重心處的截面平均應變值,不能計算其它部位,特別是最大裂縫寬度所在部位,即截面受拉邊緣處的平均應變值。而在實際工程中,最大裂縫寬度往往由外觀及人們心理上的安全感決定,所以往往需要計算截面受拉邊緣處的平均應變值。
3、剛度計算雖然基于雙折線假定,但并不是直接利用雙折線的規律進行計算,而是引進β0.4的近似擬合值進行計算。由于試驗資料的局限性,該值的計算式并沒有正確反映該值與有關參數的函數關系。
4、截面平均應變和剛度是一個統一體,但是規范方法沒有把二者有機地結合起來,而是分割開來單獨計算。
5、鋼筋混凝土受彎構件與部分預應力混凝土受彎構件屬于同一系列,鋼筋砼受彎構件可視為預應力度為零的部分預應力受彎構件,但規范采用了不同的計算公式。
6、對于多次加荷的受彎構件,當所加荷載小于以前曾施加過的最大荷載時,其截面平均應變和剛度的計算將與一次加荷時不同,而且截面平均應變值較一次加荷時大得很多。規范沒有提供這種情況下的計算公式。
本文提出的計算方法可以克服規范方法的上述缺點。
部分預應力梁開裂以后截面平均應變和剛度的直接計算法
項劍鋒 碩士、教授級高級工程師
(浙江省建筑科學設計研究院、浙江劍鋒加固工程有限公司)
提 要:本文基于截面平均應變符合平截面假定,截面彎矩與受拉邊緣處平均應變及截面曲率與受拉邊緣處平均應變的雙折線關系,利用部分預應力梁開裂以后不考慮受拉砼作用時截面上的彎矩—曲率—應變的簡化線性關系式,直接導出了開裂以后考慮受拉砼作用時截面平均應變和剛度的精度很高又很簡捷的計算公式,并通過計算例題使計算方法更加明了。
關鍵詞:彎矩、曲率、截面平均應變、雙折線、剛度、直接計算、計算例題 1 前言
在作預應力梁和鋼筋混凝土梁的撓度和裂縫寬度驗算時,主要的計算內容是開裂以后的截面平均應變和剛度。由于截面開裂以后,裂縫之間和裂縫頂部的受拉區混凝土還要承擔一部分拉力,而這部分拉力的大小和在加荷過程中的衰減速度均受許多因素影響,所以使得開裂以后的截面平均應變和剛度計算變得較為困難。
我國現行混凝土結構設計規范(GB50010-2002)采用將裂縫截面上縱向受拉鋼筋的應力(鋼筋混凝土梁)或等效應力(預應力混凝土梁)除鋼筋彈性模量乘應變不均勻系數的方法計算鋼筋重心處的截面平均應變值。裂縫截面上縱向受拉鋼筋的應力或等效應力采用簡化的內力臂計算公式計算。梁的剛度是基于彎矩曲率的雙折線假定,利用試驗資料求出  時的剛度降低系數β0.4的擬合近似值,再利用幾何關系導出M = Mk時綜合剛度的近似計算公式。 時的剛度降低系數β0.4的擬合近似值,再利用幾何關系導出M = Mk時綜合剛度的近似計算公式。
規范的這種方法,具有下述幾點不足之處:
1、簡化的內力臂計算公式沒有正確地反映內力臂與有關參數的函數關系。根據開裂截面彈性理論計算公式導出的高精度簡化式[1]知,內力臂與KS及rs二個參數成線性關系,與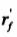 不成線性關系(Ks為縱向受拉鋼筋換算截面重心至受拉邊緣的距離與h的比值,rs為受拉鋼筋換算面積與bh的比值, 不成線性關系(Ks為縱向受拉鋼筋換算截面重心至受拉邊緣的距離與h的比值,rs為受拉鋼筋換算面積與bh的比值,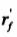 為受壓翼緣截面面積與bh的比值)。而規范公式的內力臂與 為受壓翼緣截面面積與bh的比值)。而規范公式的內力臂與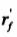 成線性關系,與ks和rs二個參數無關。 成線性關系,與ks和rs二個參數無關。
2、規范的方法只能計算縱向受拉鋼筋重心處的截面平均應變值,不能計算其它部位,特別是最大裂縫寬度所在部位,即截面受拉邊緣處的平均應變值。而在實際工程中,最大裂縫寬度往往由外觀及人們心理上的安全感決定,所以往往需要計算截面受拉邊緣處的平均應變值。
3、剛度計算雖然基于雙折線假定,但并不是直接利用雙折線的規律進行計算,而是引進β0.4的近似擬合值進行計算。由于試驗資料的局限性,該值的計算式并沒有正確反映該值與有關參數的函數關系。
4、截面平均應變和剛度是一個統一體,但是規范方法沒有把二者有機地結合起來,而是分割開來單獨計算。
5、鋼筋混凝土受彎構件與部分預應力混凝土受彎構件屬于同一系列,鋼筋砼受彎構件可視為預應力度為零的部分預應力受彎構件,但規范采用了不同的計算公式。
6、對于多次加荷的受彎構件,當所加荷載小于以前曾施加過的最大荷載時,其截面平均應變和剛度的計算將與一次加荷時不同,而且截面平均應變值較一次加荷時大得很多。規范沒有提供這種情況下的計算公式。
本文提出的計算方法可以克服規范方法的上述缺點。
2 彎矩與曲率關系曲線的雙折線假定
大量的試驗資料已表明,部分預應力砼梁和鋼筋砼梁在受拉鋼筋屈服以前,截面的彎矩—曲率關系曲線可以近似成雙折線關系,雙折線轉折點處的彎矩值為開裂彎矩Mcr(如圖1所示)。本文提出的截面平均應變和剛度的計算方法將基于這個關系,即假定所研究的梁截面在使用荷載階段,其M-Ф關系曲線具有雙折線關系。
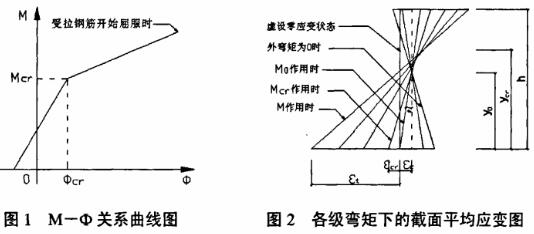
我們知道,彎矩-曲率曲線是根據試驗梁在各級彎矩下的截面平均應變的量測值畫出來的。雙折線M-Φ關系曲線的假定,實際上是將各級彎矩下的截面平均應變假定為如圖2所示。其特點是:當彎矩小于Mcr時,應變圖均相交于一點;當彎矩大于Mcr時,應變圖均相交于較高的另一點。較低的交點處即為開裂以前換算截面形心軸的位置,較高的交點處可以視為開裂以后的換算截面形心軸的位置。
3 截面平均應變和剛度的計算公式 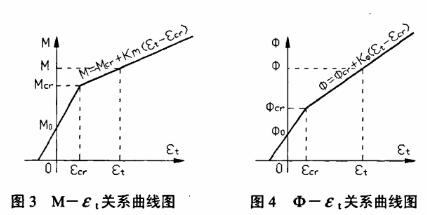
如果把圖2畫成M-εt關系曲線和Φ-εt關系曲線(εt為截面受拉邊緣處的平均應變),可以得到如圖3和圖4所示的雙折線關系。第一段直線可根據未開裂截面的幾何特征確定。雙折線法的關鍵是要確定第二段直線。如果能夠求得第二段直線的斜率,則任意一個M-Φ-εt的對應值都可以計算,從而截面上任意部位的平均應變值就可以確定;而M-εt直線的斜率除Φ-εt直線的斜率即為開裂以后的截面剛度,所以求得斜率以后也就可以同時求得剛度。因此,本文的主要任務是研究第二段M-εt直線和Φ-εt直線斜率的計算公式。
設第二段M-εt直線和Φ-εt直線的斜率分別為Km和KΦ,則直線的方程分別為:
M = Mcr+Km (εt-εcr) (3-1)
Φ=Φcr+KΦ (εt-εcr) (3-2)
由(3-1)式知:
εt =εcr+(M-Mcr)/ Km (3-3)
根據(3-3)和(3-2)式求得εt和Φ以后,可利用圖5中的幾何關系,求出截面上至受拉邊
緣距離為ax的任意部位處的平均應變值εx :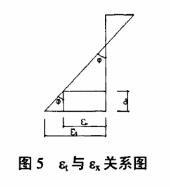
εx = εt- ax·Φ (3-4)
開裂以后的截面剛度Bcr可以按下式計算:
Bcr = Km / KΦ (3-5)
上述(3-2)~(3-5)式便是開裂以后截面平均應變和剛度的計算公式。
4 有關參數的計算公式
4.1、Km和KΦ的計算公式
由圖3和圖4知,只要能夠再定出第二段M-εt直線和Φ-εt直線上的任意一點,Km和KΦ值便可以計算。
我們知道,隨著外彎矩的增大,鋼筋所承受的拉力不斷增大,受拉區混凝土所承受的拉力在截面總拉力中所占的比例越來越小,它對截面應變的約束作用也越來越弱。如果假定在任意大荷載作用下受壓區混凝土和截面上的縱向鋼筋都不會產生塑性變形,即假定砼的抗壓強度和縱向鋼筋的屈服強度均無限高,則當截面應變增大到某一程度時,受拉區混凝土所起的作用便可以忽略不計。以彎矩與截面受拉邊緣應變的關系曲線為例,雙折線化的M-εt實測直線和按開裂截面彈性理論計算公式(即不考慮受拉混凝土作用)計算得到的M-εt關系曲線如圖6所示。二者之間的應變差值即為受拉區混凝土的作用。隨著彎矩的增大,二者的差距越來越小。由于假定受壓區砼和截面上的縱向鋼筋都不會產生塑性變形,所以隨著外彎矩的增加,二者將沿著直線的延長線上升,相交于Sˊ點(如圖6所示)。Sˊ點處的應變值即為可以忽略受拉區混凝土作用時的應變值。
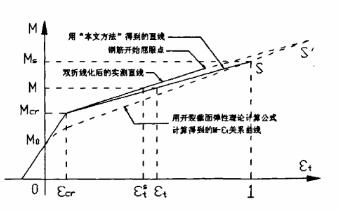
如果知道Sˊ點處的應變值,便可以根據文獻[1]中的簡化計算公式計算Sˊ點處的彎矩值和曲率值,于是便可以求出Km和KΦ值。因此,問題的關鍵是要確定Sˊ點處的應變值。
通常的做法是以受拉鋼筋開始屈服時的應變值作為Sˊ點處的應變值,如文獻[2]的做法。但是試驗資料表明,這種做法對于配置屈服強度較低鋼筋的梁截面誤差較大,因為當鋼筋開始屈服時受拉區混凝土的作用仍比較顯著,而且這種做法計算不方便,使公式中多了一個鋼筋屈服應變的參數。
為了簡化計算,本文統一以εt = 1作為Sˊ點處的應變值,即以S點代替Sˊ點(如圖6所示)。實際上,當εt = 1時,鋼筋早已屈服,受壓區砼早已破壞,所以S點并不存在,它是在假定受壓區混凝土和截面上的縱向鋼筋的強度均無限高的條件下得到的。
設截面受拉邊緣處應變εt = 1時所相應的外彎矩值為Ms,截面曲率為Φs,則Km和KΦ可以由下列公式求得:
Km = (Ms -Mcr) / (1-εcr)
KΦ = (Φs-Φcr) / (1-εcr)
由于εcr﹤﹤1,Mcr﹤﹤Ms ,Φcr﹤﹤Φs ,所以可得:
|
Km = Ms |
(4-1) |
|
KΦ =Φs |
(4-2) |
4.2、Φs和Ms的計算公式:
對于圖7所示的T形截面,文獻[1]基于開裂截面彈性理論導出了部分預應力梁開裂以后截面上的彎矩—曲率—應變的精確關系式,并借助電子計算機對各種情況下的截面作了分析,進而得出了精度很高(一般情況下誤差不大于5%)的彎矩—曲率—應變的簡化線性關系式。其表達式如下(已將原式中的RβΦ改為RΦ、Rβm改為Rm):
Φ=(R0Φ·ε0+RΦ·εt)/ h
M = NP0(R0m·h-aN)+(0.85EcA0h)·Rm·εt
式中εt—截面受拉邊緣處的截面平均應變值;
NP0—混凝土法向預應力等于零時預應力鋼筋及
非預應力鋼筋的合力;
aN—NP0至截面受拉邊緣的距離;
ε0—開裂前換算截面形心軸處的應變值。
R0Φ、、RΦ和R0m、Rm為計算系數,可查表計算。
將εt = 1代入上式,得
Φs = (R0Φ·ε0+RΦ)/ h
Ms = NP0(R0mh-aN)+(0.85EcA0h)·Rm
由于R0Φ·ε0﹤﹤RΦ NP0(R0mh-aN)﹤﹤(0.85EcA0h)·Rm
所以Φs和Ms可按下式計算:
|
Φs = RΦ/ h |
(4-3) |
|
Ms = (0.85EcA0h)·Rm |
(4-4) |
4.3、Rm、RΦ的計算公式:
根據文獻[1]的研究結果,Rm和RΦ可按下列公式計算(已將原式中的Rβ0m、Rrsm、Rksm和
Rβ0Φ、RrsΦ、RksΦ改為R1m、R2m、R3m和R1Φ、R2Φ、R3Φ):
|
RΦ = R1Φ+(R2Φ-R3Φ·Ks)γs |
(4-5) |
|
Rm = R1m+(R2m-R3m·Ks)γs |
(4-6) |
式中的R1m、R2m、R3m和R1Φ、R2Φ、R3Φ可直接從表1中查得。 式中的Ks為受拉區的預應力鋼筋和非預應力鋼筋總換算面積的形心至受拉邊緣的距離與截面高度h的比值。
式中的γs為受拉區的預應力鋼筋和非預應力鋼筋總換算面積與bh的比值。
RØ和Rm都有明確的物理意義:
Rm——開裂截面的截面抵抗矩系數:
RØ——開裂截面的形心軸位置系數:
Rm / RØ——開裂截面的剛度系數。
表1 計算系數查用表
|
系數
γfˊ |
R1m |
R2m |
R3m |
R1Φ |
R2Φ |
R3Φ |
|
0 |
0.0142 |
0.644 |
1.85 |
1.250 |
3.12 |
5.1 |
|
0.1 |
0.0118 |
0.629 |
1.69 |
1.184 |
2.62 |
4.0 |
|
0.2 |
0.0100 |
0.604 |
1.55 |
1.147 |
2.23 |
3.2 |
|
0.3 |
0.0082 |
0.576 |
1.43 |
1.126 |
1.94 |
2.7 |
|
0.4 |
0.0072 |
0.547 |
1.32 |
1.112 |
1.70 |
2.3 |
|
0.5 |
0.0063 |
0.521 |
1.24 |
1.104 |
1.51 |
2.0 |
|
0.6 |
0.0054 |
0.495 |
1.16 |
1.096 |
1.35 |
1.7 |
|
0.7 |
0.0050 |
0.470 |
1.08 |
1.092 |
1.22 |
1.5 |
|
0.8 |
0.0045 |
0.448 |
1.02 |
1.089 |
1.12 |
1.4 |
|
0.9 |
0.0044 |
0.429 |
0.98 |
1.088 |
1.03 |
1.3 |
|
≥1.0 |
0.0043 |
0.409 |
0.92 |
1.088 |
0.95 |
1.2 |
注:γfˊ為受壓區翼緣挑出部分面積及受壓區的預應力鋼筋和非預應力鋼筋的換算面積總和與bh的比值;當γfˊ處于表列數值之間時,可采用線性插值法。
4.4、ε0 、M0和εcr 、Φcr、Mcr的計算公式:
1)、ε0的計算
ε0是開裂前換算截面形心軸處的應變值,按下式計算:
ε0 = Npo/(0.85EcA0) (4-7)
2)、M0的計算
M0是使截面受拉邊緣的應力為0時所需的外彎矩值,可按下式計算:
M0 = Npo /(W0/A0+Y0-aN) (4-8)
3)、εcr的計算
εcr是相應于Mcr作用時,把截面受拉區混凝土折算成完全彈性材料后受拉邊緣處的應變值。由于受拉區混凝土在截面即將開裂時出現顯著的塑性變形,所以這是為了方便計算所虛設的值。按我國現行規范(GB50010-2002)的方法,εcr的計算公式如下:
εcr = γ·ftk /(0.85Ec) (4-9)
式中γ為截面抵抗矩塑性影響系數,按規范8·2·4條計算。
4)、Φcr的計算
Φcr是相應于Mcr作用時的截面曲率值。它也是為了方便計算所虛設的值。由圖2可以看出,Φcr可以按下式計算:
Φcr =(εcr+ε0)/ Y0 (4-10)
5)、Mcr的計算
Mcr為正截面開裂彎矩值,計算公式為:
Mcr = M0+γ·ftk·W0 (4-11)
5 工字形截面計算公式的探討
上述計算公式是根據T形截面建立起來的。對于工字形截面,由于比T形截面多出了受拉翼緣挑出部分面積,使得截面開裂以前的剛度及開裂彎矩有較大增加。在截面開裂后,由于受拉翼緣退出工作,其受力性能逐漸與T形截面接近。其彎矩—曲率曲線如圖8所示。
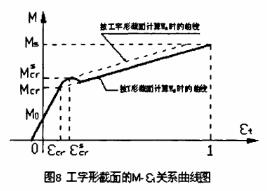
如何將工字形截面的彎矩—曲率曲線簡化成雙折線,是一個需要作進一步探討的的問題。
在計算Φs和Ms時,由于受拉翼緣已退出工作,即使中和軸還處于下翼緣內,也由于中和軸附近的應變很小,而可以忽略受拉翼緣挑出部分混凝土面積所承擔的壓力,因而可以按T形截面計算。
在計算εcr 、Φcr和Mcr時,如果按工字形截面考慮,則第二段直線將如圖8中的細虛線所示,顯然與實際曲線偏差較大,而且裂縫寬度和撓度的計算值將偏小,不安全。為了減小偏差并偏于安全考慮,筆者建議在按(4-11)式計算Mcr時,W0值按T形截面計算,不考慮受拉翼緣的作用。
|
6 多次加荷時的計算方法
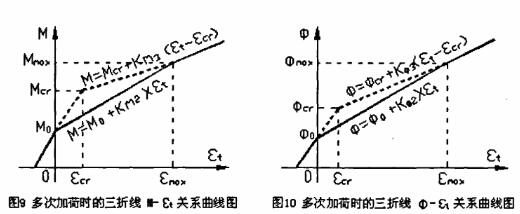
M-Ф的雙折線關系只適用于一次加荷的情況。當開裂以后,從某一荷載值卸荷并再次加荷時,M-Ф曲線將近似呈三折線關系(如圖1所示)。第一個轉折點處的彎矩值為截面受拉邊緣應變為零時的彎矩值M0,第二個轉折點處的彎矩值為以前曾作用過的荷載所產生的最大彎矩值Mmax,第一階段直線和第三階段直線均跟一次加荷時的情況基本吻合。其M-εt關系曲線和Ф-εt關系曲線如圖9和圖10所示。
設M-εt關系曲線的第2段和第3段直線的斜率為Km2和Km3 ;設Ф-εt關系曲線的第2段和第3段直線的斜率為KФ2和KФ3 。由于第1段和第3段直線均跟一次加荷時的雙折線關系曲線重合,所以Km3和KФ3及M≥Mmax以后的截面平均應變εx均可以利用一次加荷時的計算公式計算。而Km2和KФ2則可以利用圖中的幾何關系計算。公式為:
|
εmax = εcr+(Mmax-Mcr) / Km3 |
(6-1) |
|
Фmax = Фcr+KФ3(εmax-εcr) |
(6-2) |
|
Ф0 = ε0 / Y0 |
(6-3) |
|
Km2 = (Mmax-M0) /εmax |
(6-4) |
|
KФ2 = (Фmax-Ф0) /εmax |
(6-5) |
求得Km2和KФ2以后,便可以利用下述式子求M0﹤M﹤Mmax時截面底邊的平均應變和曲率:
|
εt = (M-M0)/ Km2 |
(6-6) |
|
Ф = Ф0+KФ2·εt |
(6-7) |
求得εt和Ф以后,可以利用下式求截面上至受拉邊緣距離為ax的任意部位處的平均應變εx:
截面開裂后的剛度B2按下述式子計算:
當上述方法用于實際工程時,還需要確定Mmax值。 |
7 截面平均應變和剛度的計算公式匯總
(一)7.1、一次加荷時
|
γfˊ = [(bfˊ-b)hfˊ+npˊ·Apˊ+nsˊ·Asˊ]/ bh |
(7-1) |
|
γs = (np·Ap+ns·As)/ bh |
(7-2) |
|
Ks = (np·Ap·ap+ns·As·as)/[( np·Ap+ns·As)·h] |
(7-3) |
|
Rm = R1m+(R2m-R3m·Ks)·γs |
(7-4) |
|
RФ = R1Ф+(R2Ф-R3Ф·Ks)·γs |
(7-5) |
|
ycr = h / RФ≦h-hfˊ |
(7-6) |
若ycr﹥h-hfˊ,則應按b = bfˊ的矩形截面重新計算。
|
ε0 = Np0 /(0.85EcA0) |
(7-7) |
|
εcr = (γ·ftk)/ 0.85Ec |
(7-8) |
|
Ф0 =ε0 / Y0 |
(7-9) |
|
Фcr = (ε0+εcr)/ Y0 |
(7-10) |
|
M0 = Np0(W0 / A0+y0-aN) |
(7-11) |
|
Mcr = M0+γ·ftk·W0 |
(7-12) |
|
Wcr =Rm·A0h |
(7-13) |
|
εt =εcr+(M-Mcr)/( 0.85Ec Wcr) |
(7-14) |
|
Ф = Фcr+(εt-εcr)/ Ycr |
(7-15) |
|
εx =εt-ax·Ф |
(7-16) |
|
B3 = 0.85Ec·Wcr·Ycr |
(7-17) |
(二)7.2、多次加荷時
|
εmax =εcr+(Mmax-Mcr)÷(0.85Ec·Wcr) |
(7-18) |
|
Фmax = Фcr+(εmax-εcr)/ ycr |
(7-19) |
|
εt = (M-M0)÷(Mmax-M0)·εmax |
(7-20) |
|
Ф = Ф0+εt /εmax·(Фmax-Ф0) |
(7-21) |
|
εx = εt-ax·Ф |
(7-21) |
|
B2 = (Mmax-M0)÷(Фmax-Ф0) |
(7-22) |
8 計算例題
截面形狀和尺寸如圖11所示。已知使用階段時截面上所有鋼筋在砼法向預應力等于零時的合力Np0 = 857KN;砼、預應力鋼筋和非預應力鋼筋的彈性模量分別為Ec = 3.25×104N/mm2、Ep = 1.95×105N/mm2、Es = 2×105N/mm2;砼的標準抗拉強度ftk = 2.39 N/mm2。試計算:初次加荷和多次加荷M = 700KN·m時,截面底面和非預應力鋼筋重心處的截面平均應變值,及截面開裂以后受拉鋼筋屈服以前在初次加荷和多次加荷時的剛度。設該截面曾作用過的最大彎矩值為M*max = 840KN·m。
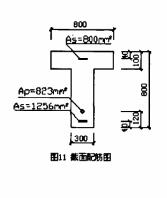
[解]
1、 求截面幾何特征值和基本計算量:


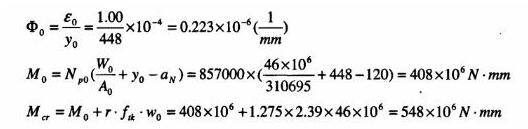
2、根據γfˊ= 0.232由表1查計算系數,查得:
R1Ф = 1.140 R2Ф = 2.14 R3Ф = 3.0
R1m = 0.0094 R2m = 0.595 R3m = 1.51
3、求RФ和Rm:
RФ = R1Ф+(R2Ф-R3Ф·Ks)γs = 1.140+(2.14-3.0×0.089)×0.062 = 1.256
Rm = R1m+(R2m-R3m·Ks)γs = 0.0094+(0.595-1.51×0.089)×0.062 = 0.0380
4、求Фs和Ms :
Фs = RФ/ h = 1.256÷800 = 0.00157
Ms = (0.85EcA0h)·Rm = 0.85×3.25×104×310695×800×0.0380 = 0.26×1012 N·mm
5、檢驗中和軸位置:
Kh = 1/Фs = 1/0.00157 = 637mm﹤800-100 = 700mm
中和軸尚未上升到受壓區內
6、求Km3和KФ3 :
Km3 = Ms = 0.26×1012N·mm
KФ3 = Фs = 0.00157(1/mm)
7、求初次加荷M = 700KN·m時截面底部和非預應力鋼筋重心處的平均應變εt和εs :
εt = εcr+(M-Mcr)/ Km3
= 110×10-6+(700×106-548×106)÷(0.26×1012) = 695×10-6
Ф = Фcr+KФ3(εt-εcr)
= 0.469×10-6+0.00157×(695-110)×10-6 = 1.39×10-6(1/mm)
εs =εt-as·Ф = 695×10-6-40×1.39×10-6 = 639×10-6
8、求初次加荷開裂以后的剛度B3 :
B3 = Km3 / KФ3 = 0.26×1012÷0.00157 = 166×1012N·mm
9、求多次加荷M = 700KN·m時的εt和εs :
εmax =εcr +(Mmax-Mcr) / Km3
= 110×10-6+(840-548)×106÷(0.26×1012) = 1233×106
Фmax = Фcr+KФ3(εmax-εcr)
= 0.469×10-6+ 0.00157×(1233-110)×10-6 = 2.23×10-6
Km2 = (Mmax-M0) /εmax
= (840-408) ×106÷(1233××10-6) = 0.35×1012
KФ2 = (Фmax-Ф0) /εmax
= (2.23-0.223) ×10-6÷(1233××10-6) = 0.00163
εt = (M-M0) / Km2 = (700-408)×106÷(0.35×1012) = 834×10-6
Ф = Ф0+KФ2·εt = 0.223×10-6+0.00163×834×10-6 = 1.58×10-6(1/mm)
εs = εt-as·Ф = 834×10-6-40×1.58×10-6 = 771×10-6
10、求開裂以后多次加荷時的剛度B2 :
B2 = Km2 / KФ2 = 0.35×1012÷0.00163 = 215×1012N·mm
9 結束語
本文基于截面平均應變符合平截面假定,截面彎矩與受拉邊緣處平均應變及截面曲率與受拉邊緣處平均應變的雙折線關系,利用部分預應力梁開裂以后不考慮受拉混凝土作用時截面上的彎矩—曲率—應變的簡化線性關系式,直接導出了開裂以后考慮受拉混凝土作用時截面平均應變和剛度的計算公式。這些計算公式除了形式簡單、計算工作量少外,還具有下述特點:
1、由于簡化計算式正確地反映了截面彎矩、曲率、應變與各有關參數的函數關系,所以計算結果的精度較高;
2、所建立的公式不僅對部分預應力受彎構件適用,對鋼筋混凝土受彎構件和大偏心受壓構件也適用;
3、可以計算截面上任意部位的截面平均應變值,因而可以計算截面任意部位處的裂縫寬度值;
4、可以同時計算截面平均應變和剛度,使得裂縫寬度計算和撓度計算連成一體;
5、不僅可以計算一次加荷時的截面平均應變和剛度,還可以計算多次加荷時的截面平均應變和剛度,符合構件的實際使用情況。
參考文獻
[1] 項劍鋒:“部分預應力梁不考慮受拉混凝土作用時截面應變的計算”,《建筑結構學報》,1983年第4期,P34~45。
[2] R.F.Warner,“Serviceability of Cracked Prestressed Concrete Members: Tests and Analysis”。FIP Symposia onPartial Prestressing .1980. Bucharest. Romania, Procedings : Part I. |